Coordenadas de un punto

Video-56 Coordenadas Polares - Trigonometria

Distancia entre dos puntos

DISTANCIA ENTRE 2 PUNTOS

DEFINICION: 

Esla longitud de un segmento de recta. Dados los puntos P1 (x1) y P2 (x2) en la recta nùmerica.

Para calcular la distancia que existe de un punto A a un punto B dadas sus coordenadas. Trabajamos con la fòrmula:

donde x2 = al valor de B en el eje de las "x" y y2 = al valor de B en el eje de las y o viceversa.

EJEMPLO:

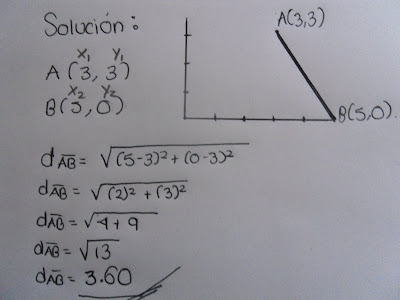
Localice la distancia entre los puntos, de las siguientes coordenadas:

A(3,3) y B(5,0)

SISTEMA DE COORDENADAS POLARES

DEFINICION: El sistema polar es similar al cartesiano, su objetivo es la representaciòn gràfica de elementos geomètricos, utilizando un segmento y un àngulo, tal segmento recibe el nombre de radio y el àngulo: argumento.

SIGNOS DE LAS COORDENADAS DE UN PUNTO EN EL SISTEMA POLAR:

1) El argumento se considera positivo si su giro es en sentido contrario al de las manecillas del reloj.

2) El argumento se considera negativo si su giro es en el mismo sentido al de las manecillas del reloj.

GRÀFICA DE UN PUNTO EN COORDENADAS POLARES:

CASO 1: Si el radio vector es positivo (r > 0)

Se mide "r" a la derecha del polo y se gira el nùmero de grados segùn lo insique el àngulo; este se mide partiendo del lado positivo del eje polar y girando en sentido opuesto al de las manecillas del reloj.

CASO II: Si el radio vector es negativo (r < 0)

Se mide "r" a la izquierda del polo y se gira el nùmero de grados segùn lo indique el àngulo; èste se mide partiendo del lado negativo del eje polar y girando en sentido opuesto al de las manecillas del reloj. 

EJEMPLOS:

Gràfica el punto (6, 150º)

SOLUCIÒN: Sobre el eje polar se traza el radio vector con magnitud 6 hacia la derecha del polo, y se gora 150º en sentido contrario al de las manecillas del reloj.

Gràfica el punto (-3, 120º)

SOLUCION: Sobre el eje polar se traza el radio vector con magnitud 3 hacia la izquierda del polo, y se gira 120º en sentido contrario al de las manecillas del reloj.

SISTEMA DE COORDENADAS RECTANGULARES

En el sistema de coordenadas, tomaremos como base dos rectas perpendiculares, cuyo punto de intersecciòn se denomina origen. La recta orizontal recibe el nombre de eje X (eje de las absisas), y la recta vertival recibe el nombre de eje Y ( eje de las ordenadas).


El plano cartesiano esta dividido en 4 regiones llamadas cuadrantes. A cada punto P se les asigna un par ordenado o coordenada P (x,y)

Para localizar un punto P (x,y) en el plano cartesiano se roma como referencia el origen, avanzando tanto como lo indique el primer nùmero (absisa) hacia la derecha o izquierda segùn sea su signo, de este punto se avanza hacia arriba o hacia abajo, tanto como lo indica el segundo nùmero (ordenada) segùn sea su signo.

PROPÒSITOS

Mostrar una visiòn global del mètodo de la Geometrìa Analitica como el medio para resolver problemas de corte euclidiano reducièndolos a problemas algebraicos.